Good morning. SGO Technology Institute is. Best wishes for a Happy New Year!! :)

Today,  I will introduce spherical bearings .

A spherical bearing is a  bearing in which the journal portion of the bearing
has a sphere shape. In the case of an oilless bearing, the surface where the sliding motion occurs is formed in a sphere shape.

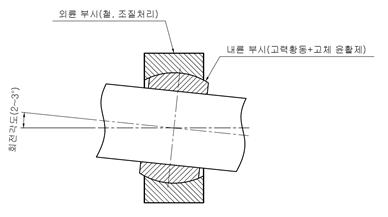
In the picture above, you can see that the inner ring bush (I.D Bush), which is the body of the oilless bearing embedded with solid lubricant, has a  spherical shape.

The inner ring bush is a type in which a solid lubricant is embedded in a high-strength brass, and is generally constructed by being assembled with an outer ring bush (O.D Bush) that serves as a housing.

Depending on the application, solid lubricant may be embedded in the outer ring bush, or solid lubricant may be embedded in both the inner and outer ring bushes.

​

The reason for using spherical bearings is that by enabling the rotation of the shaft connected to the inner ring bush, it can withstand loads acting in various directions or absorb shocks and vibrations . 

In the'Oilless Bearing Durability Test Method', which was posted last time, the surface pressure was calculated for the load acting only in the radial direction of the bearing.

In contrast, spherical bearings have the effect of attenuating impact, vibration, and friction by forming a stable surface pressure even under loads acting in the axial direction (thrust) . 

​

The rotation angle is usually very small by 2~3 degrees, but sometimes it passes a steep inclination angle of up to 15~25 degrees, and accordingly, the rotation angle and the size of the inner ring bush are designed to be proportional.

The surface pressure of a spherical bearing can be calculated by the following equation.

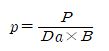
p = surface pressure (N/㎟)

p = equivalent radial load (N)

Da = diameter of inner ring bush (mm)

B = width of outer ring bush (mm)

​

The equivalent radial load corresponding to P is a value obtained by substituting the radial load for the effect of the load acting in the axial direction, and can be calculated by the following equation.

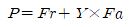
P = equivalent radial load (N)

Fr = radial load (N)

Fa = thrust load (N)

Y = axial load factor

※Standard table of axial load factor

In addition, the sliding speed of the bearing can be calculated by the following equation.

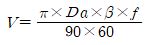
V = sliding speed (mm/sec)

β = swing half angle (degree, half of rotation angle)

f = number of oscillations per minute (times/minute)

However, this is an equation calculated under the assumption of ideal conditions, and it is different from the actual environment because it can be affected by various factors (whether or not using lubricant, conditions of use, environment and frequency, etc.).

Therefore, please use it for reference purposes only. :)

​

If you have any questions about this, please feel free  to contact SGO R&D Center !